|
|
|
|
The Minesweeper update you've been waiting for. |
|
Welcome! Total Minesweeper™ is a new Minesweeper-based game.
It differs from the original Minesweeper by showing the total count of unflagged mines in each row and column of the grid. To compensate, the game begins with a larger number of mines. This changes the gameplay, leading to less guessing and more calculations. The "total" part of the name comes from the fact that rows and columns totals can be often used to solve the puzzle. In this little tutorial I demonstrate some examples of this. In all examples we assume that colums and rows are numbered from left to right and from top to bottom, starting with one. Numbers to the left of rows and on top of the colums represent the total number of unmarked mines (bombs) in a given row or column. No number means zero. Disclaimer: in some examples below there's more than one way to make your next move. In some cases however, using totals is the only way to avoid guessing. For Minesweeper rules please reference this site. Example 1.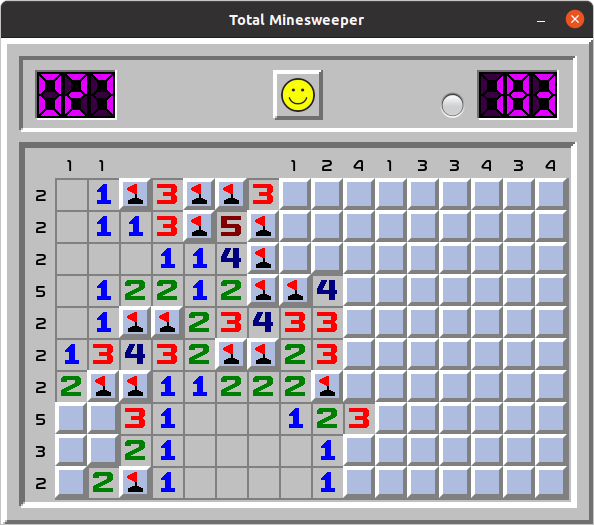
We note that in column 8 its single unmarked mine must be in rows 1-2. This leaves cell at row 3 (shown in green) empty and safe to open. See the image below: 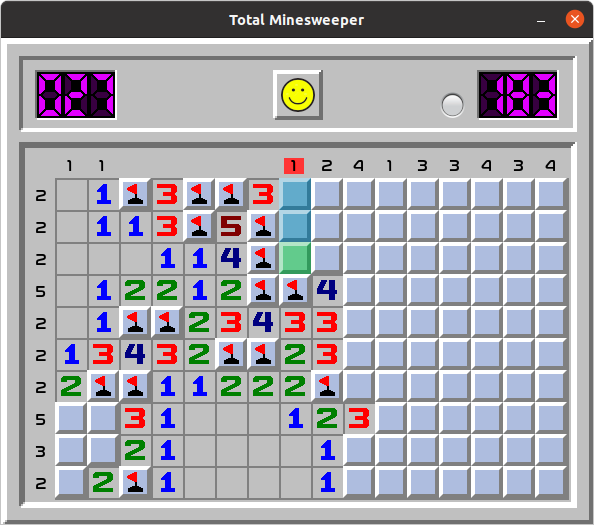
We also can notice that another column, #11, has just one mine. From the 3x3 group of cells centered at row 8 of column 10, we conclude that this single mine must be located in one of three cells in rows 7-9 (marked darker blue). This means we can safely open all remaining seven(!) cells in column 11. Refer to the image below: 
Example 2.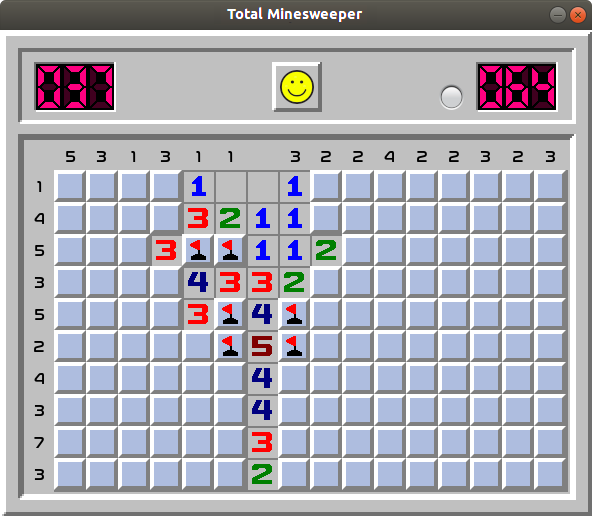
Column 9 contains only two mines. One of them is in rows 1-2 and another in rows 4-5. This means all remaining five cells of column 9 starting from row 6 are safe to open! 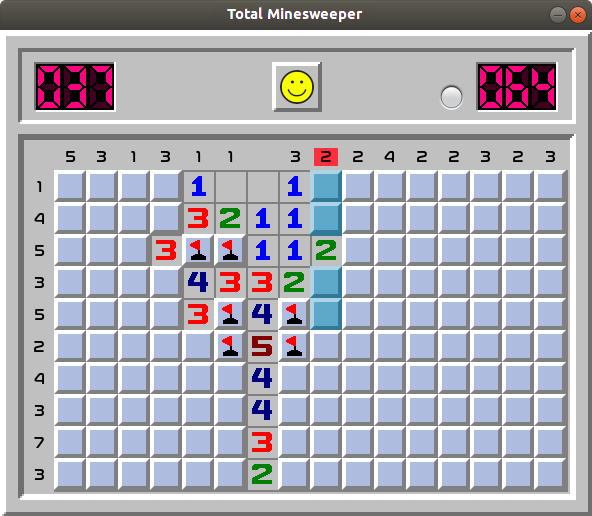
Also, we can notice that columns 6 and 8 have a total of four mines combined. These four mines are all located in 3x3 block around cell at row 8 in colum 7 (darker blue below) leaving the two bottom cells in row 10 (marked green) safe to open. 
Example 3.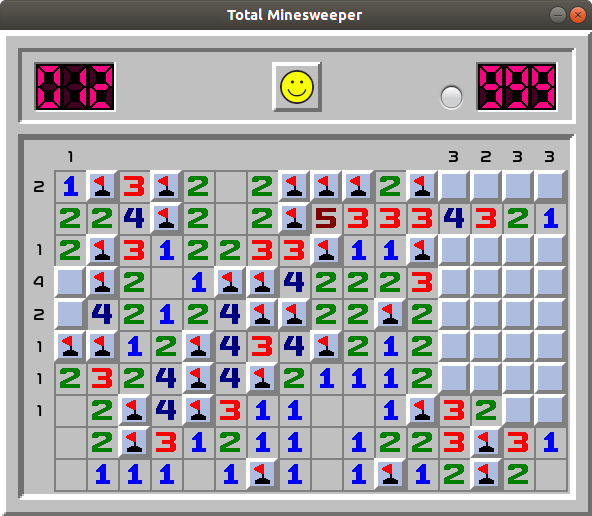
Here column 13 (fourh from the right) has three uncovered mines. Let's group cells in this column to determine where some of them are. The two cells in rows 1 and 3 have one mine between them; also three cells in rows 4-6 (marked in green below) have another mine. This leaves the last, third mine of column 13 in row 7 (marked as red). 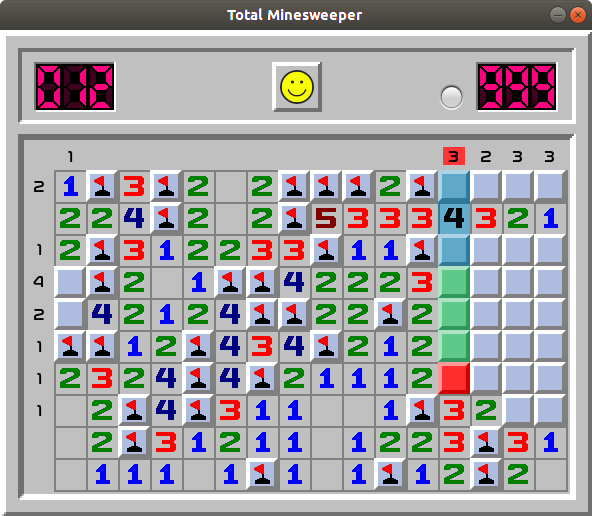
We can group the cells in our column 13 a bit differently to find out that cell at row 4 also contains a mine: 
Example 4.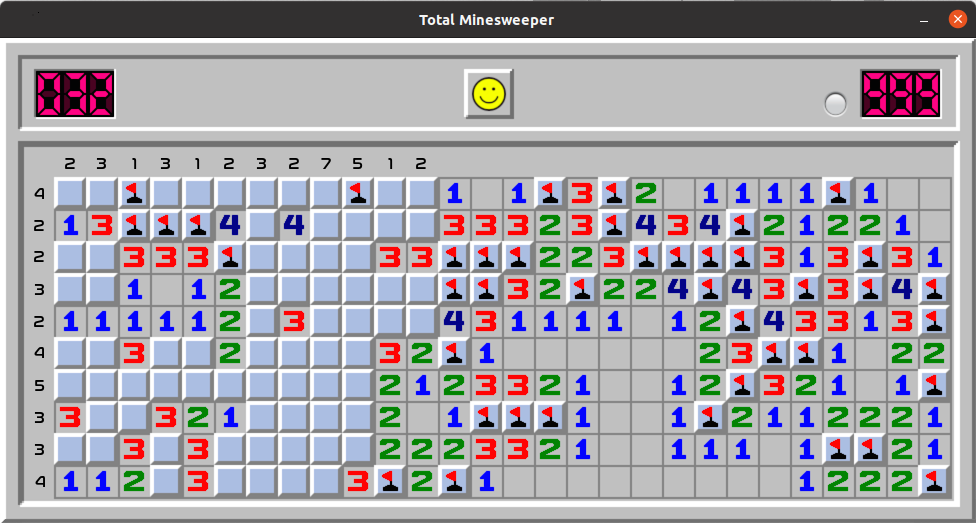
This case is more complex and involves calculations of totals in both rows and columns. The bottom row 10 contains 4 mines in its 5 unopened cells. Can we determine which of the five cells have mines? We observe that colums 5, 6 and 7 have a total of 6 uncovered mines combined. In these 3 colums:
This leaves the last, 6th mine present at the bottom row in colums 6 or 7. From this, we deduct that in the bottom row 10 remaining three colums 4, 8 and 9 all contain mines. They are marked in red on the image below. 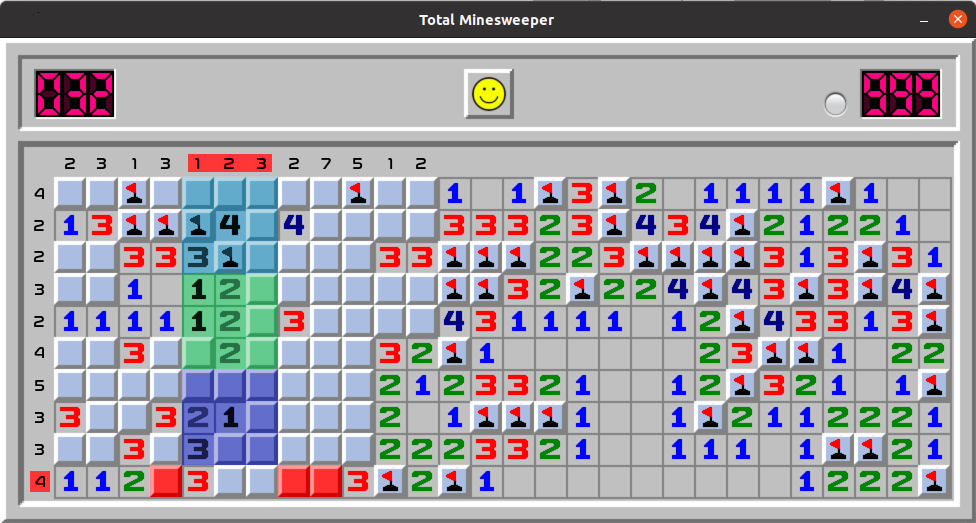
Alternatively, we can group cells in columns 2-4 containing a total of seven unmarked mines, to show that two closed cells in row 1 (columns 2 and 4) are safe to open. I will leave it to you this as a small excercise. Example 5.This is the later stage of the game from Example 4.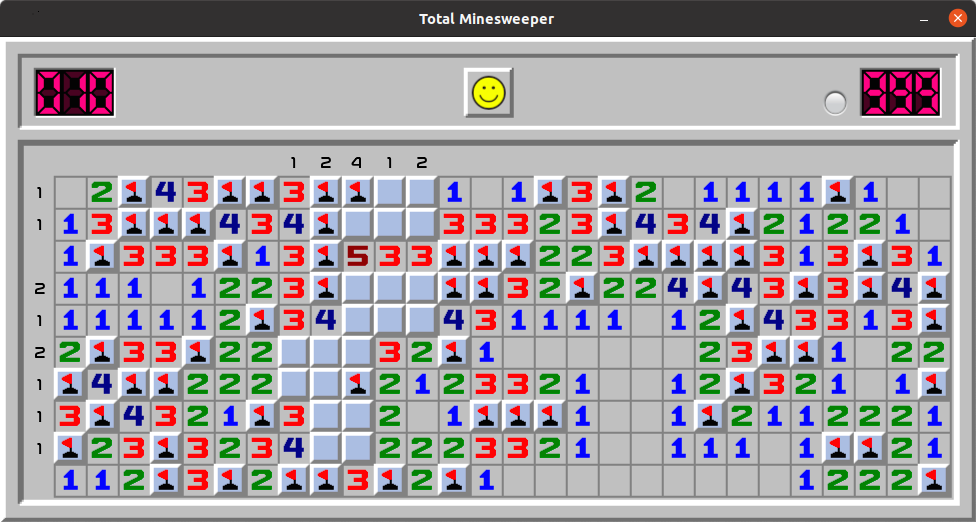
We observe that column 10 has 4 uncovered mines. One of them is located at rows 8-9; two more are located at rows 4-6, leaving the 4th mine at row 2 of column 10 (marked in red). We also notice that in row 6, containing just 2 uncovered mines, one of them is located in columns 8-9 (green), leaving the only unopened cell in this row with a mine. It is also marked in red. 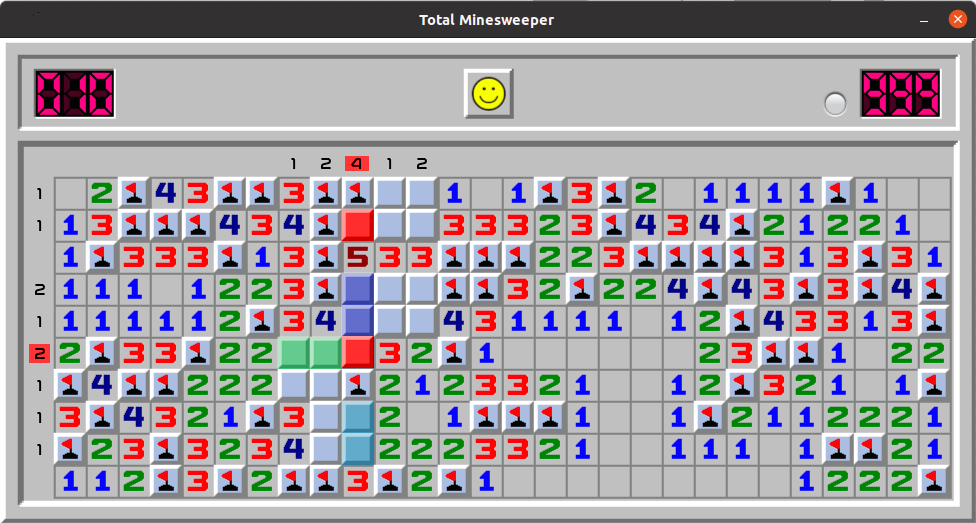
Example 6.This final example is about using probability to make better guesses when you have to.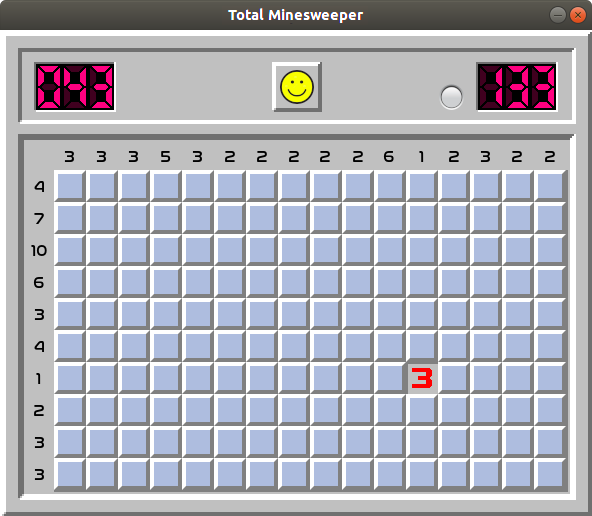
Imagine a rectangular block of unopened cells as in the image above. Any cell can contain a mine, and you lose the game if you open such cell (we pretend that "safe mode", preventing you from stepping on a mine right away is turned off). With classic Minesweeper, in this case you have to guess. With Total Minesweepr™ you can use rows and columns totals to minimize your chances of stepping on a mine. In our case, we select a cell with the smallest row and column total. Similar considerations should be used when among several rows with equal or almost equal number of unopened cells there is a row with much smaller total. You can minimize your chances of losing by opening a cell in this row. Some final words.The game is available on Mac, Windows, Ubuntu Linux, iOS and Android.All versions are free. The default "Beginner" level when you first install the game is quite simple. If you are a seasoned Minesweeper player, you can easily move to the next level or even to the custom level which goes up to 30% density. On average it becomes more interesting when mine density goes over 25%. I hope you enjoy this game as much as I do. Don't forget to subscribe to my Reddit where I will be occationally posting some news and updates. |